Interpretace výsledků fMRI

Statistické parametrické mapy, testovací hypotézy

Korekce pro mnohonásobná testování

Interpretace aktivačních map a dalších výsledků

Statistické parametrické mapy, testovací hypotézy

Jako výsledek voxel-by-voxel detekční metody získáváme tzv. statistickou parametrickou mapu (SPM = statistical parametric map), resp. neparametrickou u neparametrické statistiky. Proto se tento postup statistické analýzy označuje jako statistické parametrické (resp. neparametrické) mapování. Získaná statistická mapa obsahuje v každém bodě hodnotu statistiky pocházející z příslušného rozdělení, např. t-hodnoty u Studentova rozdělení. Takováto mapa je však pro orientaci a hodnocení nevýhodná. Provádíme tedy její prahování, to znamená, že pro každý bod musíme rozhodnout o významnosti či nevýznamnosti statistické hodnoty v tomto bodě. K tomu stanovujeme tzv. nulovou a alternativní hypotézu a hladinu významnosti na níž provádíme test rozhodující o přijetí či zamítnutí nulové hypotézy. Jako nulovou hypotézu určíme např., že průměrná hodnota signálu při stimulaci se neliší od průměrné hodnoty signálu v klidovém stavu. Alternativní hypotéza pak říká např., že hodnota při stimulaci je větší než v klidu. Hladina významnosti je pak pravděpodobnost s jakou ještě připustíme, že můžeme zamítnout nulovou hypotézu, ačkoliv ve skutečnosti platí. Kontrolujeme podle ní statistickou chybu I. druhu a obvykle se u běžných testů volí p=0,05. Takováto hladina významnosti se ovšem pro fMRI hodí jen v některých případech, o čemž bude řeč v následujících podkapitolách. Na následujících obrázcích vidíme původní statistickou mapu, výsledek po jejím prahování a nakonec přeložení přes T2*-vážený snímek mozku.

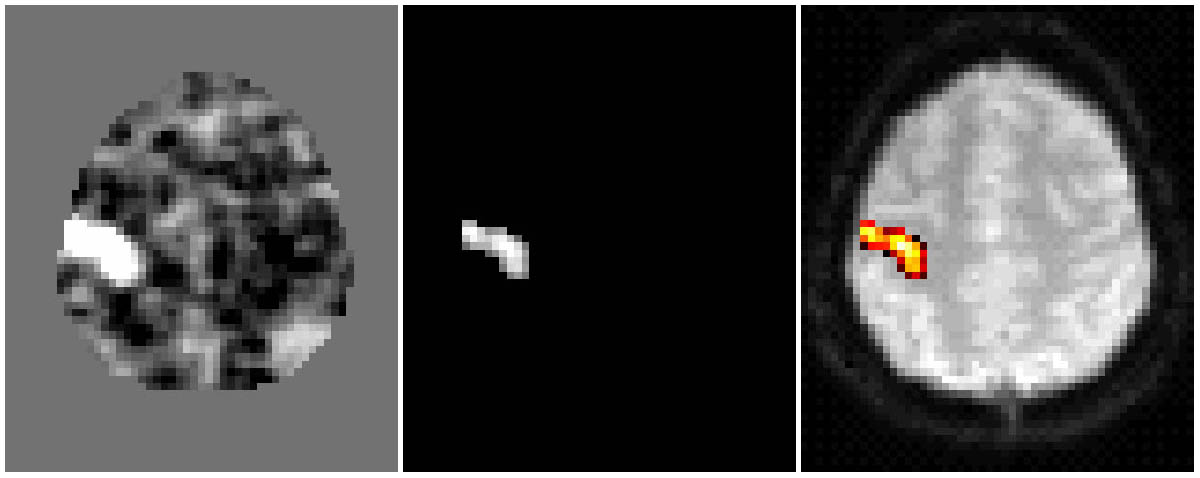
K hodnotě, která určuje prahovací mez (statistika v daném bodě ji musí překročit, abychom ji ponechali jakožto významnou), se dostaneme použitím příslušného pravděpodobnostního rozdělení a zvolené hladiny významnosti. Tato nám vlastně udává procento plochy pod křivkou rozdělení. Dle kladené otázky, neboli volby nulové a alternativní hypotézy, rozlišujeme tzv. jednostranný a oboustraný test. V případě jednostranného testu uvažujeme jako možné alternativní případy jen ty, kdy je zjištěná hodnota významně větší, popř. významně menší (pouze jedna posuzovaná možnost) než uvažovaná střední hodnota zkoumaného rozdělení naměřených dat. Pak hledáme prahovou hodnotu pouze na jednom konci rozdělení. Naopak u oboustranného testu se ptáme na to, zda je porovnávaná hodnota dostatečně vzdálená od střední hodnoty (tedy větší nebo menší, zkoumáme oba stavy). Pak musíme hladinu významnosti, tedy plochu pod křivkou, rozdělit rovnoměrně na oba konce křivky - kontrolujeme oba směry odlišnosti od střední hodnoty. 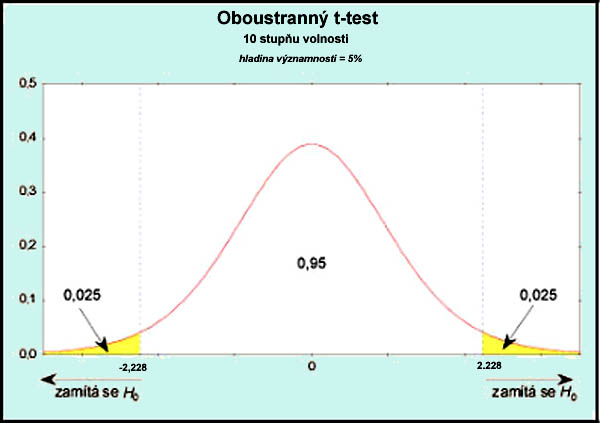V tomto případě (naznačeném také na následujícím obrázku) bude nalezená prahová hodnota větší než v případě jednostranného testu.

Korekce pro mnohonásobná testování

V případě použití voxel-by-voxel analýzy nezávisle a současně testujeme hypotézu pro mnoho testů (pro každý voxel v mozku provádíme jeden test). Pokud bychom ve fMRI použili běžné hladiny významnosti (např. 0,05), pak výsledná chyba platná pro celý mozek bude n-násobně větší (n je počet testovaných voxelů v mozku). Z tohoto důvodu je nutné ve fMRI stanovovat podstatně přísnější prahování (nižší hladinu významnosti) k čemuž se používají různé korekce pro mnohonásobné testování, např. Bonferroniho korekce. Teprve prahovanou statistickou mapu považujeme za výslednou mapu detekovaných aktivací a tuto následně použijeme k hodnocení výsledku experimentu.

Jako nekorigovaná hladina významnosti se často používá hodnota 0,001 (popř. 0,0001), která se uplatní při zkoumání předem definovaných oblastí zájmu, popř. při průzkumu celého mozku z hlediska rozložení masivnosti aktivací a množství artefaktů či šumu.

Ke korekci se v současnosti používají dvě metody. Jedná se o tzv. FWE (family wise error) korekci, při níž kontrolujeme pravděpodobnost výskytu falešně pozitivního výsledku v celém souboru testovaných voxelů a tzv. FDR (false discovery rate) korekci, při níž kontrolujeme poměrné množství falešně pozitivních výsledků. Každá z těchto korekčních metod pak nabízí několik možných implementací / mechanizmů pro výpočet skutečně použité rozhodovací hladiny významnosti. Jen stručně si zmíníme, že např. FWE může být implementována pomocí Bonferroniho korekce (uvažujeme skutečně nezávislé testy, výslednou hladinu pravděpodobnosti získáme ze zadané podělením počtem testů - tedy testovaných voxelů) nebo pomocí tzv. 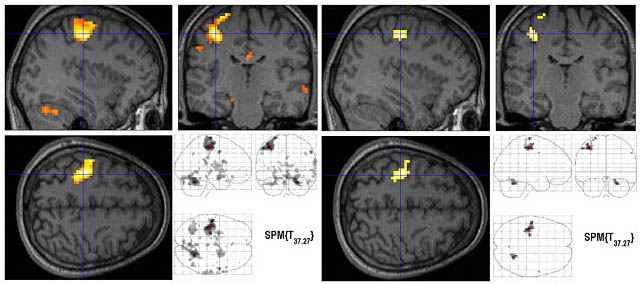"teorie náhodných polí" (RFT = Random Fields Theory; měří míru nezávislosti voxelů v mozku a ke korekci se použije jen počet skutečně nezávislých voxelů, tzv. resselů). Na následujícím obrázku vidíme vlevo použití nekorigovaného prahu p < 0,001 a korigovaného prahu pomocí FWE pro p < 0,05.

Interpretace aktivačních map a dalších výsledků

Po získání aktivační mapy nastupuje krok, v němž je třeba provést interpretaci výsledků a to především interpretaci neuroanatomickou. Jedná se o posouzení lokalizací jednotlivých aktivovaných oblastí vzhledem k funkční anatomii mozku, dále o srovnání statistických hodnot mezi jednotlivými oblastmi a také např. o zjištění určitých časových sousledností v průběhu hemodynamických odpovědí u těchto oblastí. Z těchto informací lze následně sestavit i celkový model funkční aktivace (tedy návaznost mezi postupným zapojováním jednotlivých oblastí do řešení odpovědi na stimulaci) např. pomocí modelů funkční konektivity

Základním krokem interpretace bývá lokalizace funkčních oblastí. Tuto můžeme provádět na základě přeložení aktivační mapy přes podrobné anatomické snímky (což vyžaduje jejich nasnímání a provedení vzájemné registrace s funkčními daty), kdy je k popisu nutná dobrá orientace v anatomii lidského mozku nebo na základě porovnání lokality s atlasem mozku (což vyžaduje provedení prostorové transformace do stereotaktického prostoru shodného s atlasem). 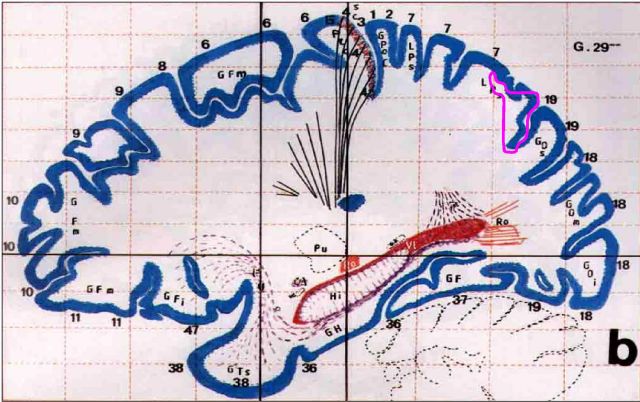Prakticky se obě metody kombinují, pouze pro výstup se zachováním původních anatomických proporcí se musí lokalizace opírat jen o podkladové strukturální snímky. Na následujícím obrázku je vidět ohraničení aktivní oblasti (souvislého shluku voxelů = tzv. klastru) přenesené do Talairachova atlasu.

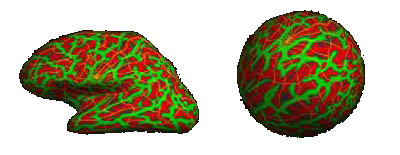
Speciálním případem transformace je využití reprezentace v kortikálních plochých mapách místo pouhé normalizace k šabloně průměrného mozku. Výhodou takového přístupu je zobrazení výsledků celé hemisféry na jediném 2D snímku. Princip si můžeme představit tak, že každá hemisféra je nafouknuta do té míry, až se rozbalí všechny kortikální závity a získaný povrch pak prezentujeme rozložením do jediné roviny ve 2D obraze. Ukázku plochých kortikálních map můžeme vidět na následujícím obrázku.

Porovnávání aktivací z hlediska rozsahu aktivované oblasti a velikosti statistických hodnot závisí na použité statistice, prahování a příslušných korekcí, a je třeba si uvědomit, že neurovědci je zde ponechána velká volnost. Především volba správného prahu a použití dodatečných korekcí pro mnohonásobné testování je krok na nějž nelze vytvořit jednoznačné pravidlo a při hodnocení je nutné využívat i osobních zkušeností a určitého "expertního" náhledu na konkrétní problematiku. Velikost statistických hodnot v jednotlivých voxelech je někdy interpretována jako síla aktivace, což je označení ne zcela přesné. Je třeba si uvědomit, že při využití regresního modelu a následném odhadu parametrů regrese může být jejich velikost (označována také jako síla efektu) ovlivněna jednak velikostí změny amplitudy sledovaného signálu a jednak shodou časování modelového a měřeného průběhu (tedy posunutím mezi modelem a měřenými daty). Tuto dvojznačnost nelze postihnout přímo testovou statistikou a musíme se na ni zaměřit až při hodnocení výsledku a následné verifikaci provedených statistických šetření a použitých výchozích předpokladů.

Na závěr se zmíníme o tom, že interpretace se ne vždy zakládá na aktivační mapě vycházející ze statistického srovnání BOLD efektu s průběhem experimentu. Další možností je zobrazení závislosti detekovaného efektu na dalším parametru, např. na obtížnosti určitých stimulů vůči jiným, či závislosti na pořadí a čase prezentace jednotlivých stimulů. Můžeme tak sledovat např. určitou "akumulaci" efektu v závislosti na doplňkovém parametru, zobecněně tedy lokality s určitou závislostí změn aktivace.