Statistická analýza (Detekce aktivace)
Úvod, přehled metod
Naprostá většina prakticky používaných metod pro detekci aktivace je založena na jednorozměrné statistice. K detekci lze použít i takové metody jako je analýza hlavních komponent atd., avšak tyto nám nedokážou dát informaci o tom jak pracuje mozek ani nám nedovolují pokládat specifické otázky. Proto se téměř nepoužívají.
Většina voxel-by-voxel metod jednorozměrné statistiky vyžaduje ke své činnosti tvorbu modelu popisujícího předpokládaný průběh hemodynamické odezvy na základě znalosti experimentální stimulace. Určitým mezikrokem je pak dekonvoluce, která vyžaduje pouze znalost začátků opakujících se událostí. Nyní si uvedeme stručný přehled jednorozměrných metod a následně budou některé z nich podrobněji vysvětleny
- korelace
- t-testy
- ANOVA
- AnCova
- lineární regrese
- vícenásobná regrese
- F-testy
- atd ...
Všechny výše uvedené metody je možné realizovat jako speciální případy obecného lineárního modelu (GLM = general linear model). Jedná se o tzv. parametrické metody, kdy předpokládáme určité chování naměřených dat, např. normální rozložení reziduí. Zejména v případě, kdy toto neplatí lze použít také metody neparametrické.
t-testy
Nejjednodušší přístup (a také nejnáchylnější na různé artefakty a citlivý na
kvalitně získaná nezašuměná data) je prostý rozdíl průměrné hodnoty signálu
získaného v době aktivity a průměrné hodnoty signálu získaného v době klidu.
O něco lepší výsledky jsme schopni získat použitím srovnání těchto průměrů
studentovým t-testem, kdy je rozdíl průměrů navíc "vážen" směrodatnou odchylkou.
Bereme tak v úvahu již i variabilitu dat, čímž se vyhneme některým falešně pozitivním detekcím.
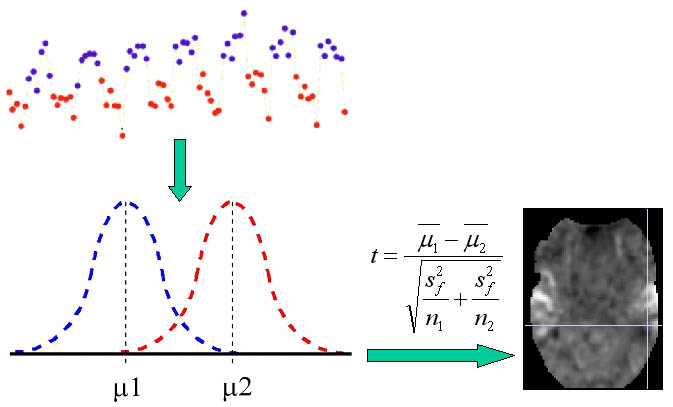
Korelace a regrese
O další stupeň výše stojí metody, které předpokládají jistý tvar měřeného
signálu (modelujeme hemodynamickou odpověď dle znalostí průběhu experimentální
stimulace). Zde se nabízí použití korelační a regresní analýzy.
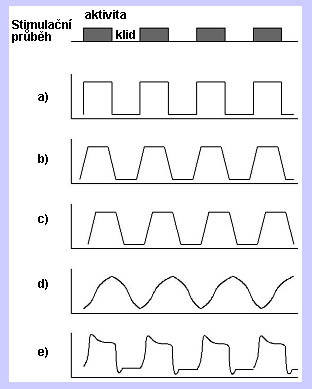
Na předchozím obrázku můžeme vidět průběh stimulační funkce (jednoduchý blokový design)
a několik možných modelových průběhů. Základním (a) je periodický obdélníkový
průběh odvozený od průběhu stimulace. Dále můžeme uvažovat (b) pozvolný náběh
a sestup naměřeného signálu, (c) jistou setrvačnost atd. Odezvu lze také
modelovat pomocí funkcí (d) jako sin, cos, apod. Nejdokonalejším způsobem z
hlediska napodobení skutečné fyziologie je (e) konvoluce experimentálního
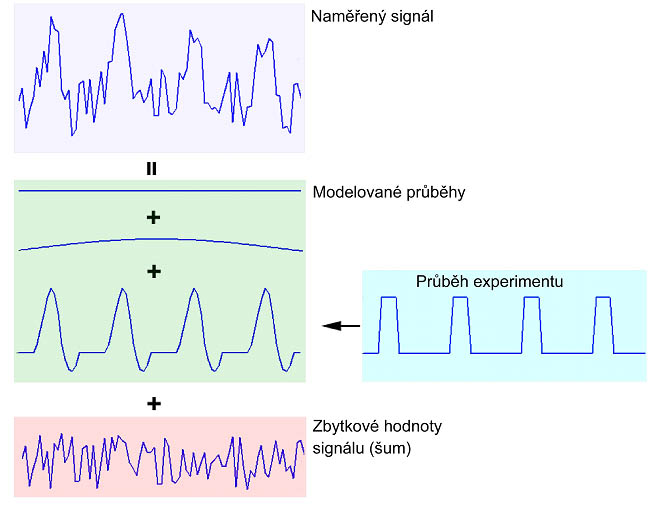
průběhu s hemodynamickou funkcí. Na dalším obrázku pak můžeme vidět naznačený
princip jednoduché lineární regrese, kdy naměřená data jsou modelována jako
součet konstantního členu, násobku modelové funkce a vektoru reziduí
(zbytkové variability v datech).
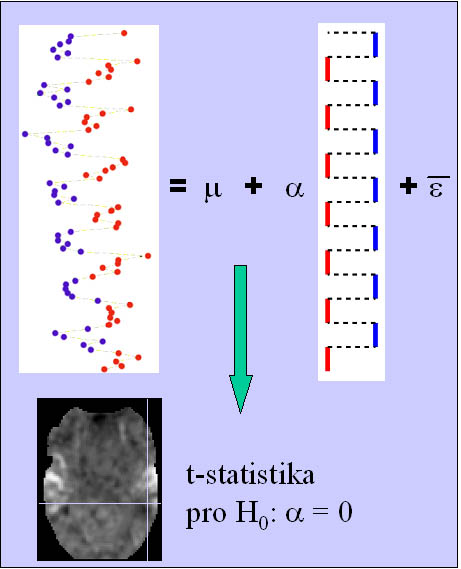
Regresní analýzou tak získáváme již poměrně flexibilní nástroj, kdy se pokoušíme vysvětlit chování variability v datech pomocí jednotlivých regresorů (modelů možné či předpokládané odezvy na určité typy stimulů) a následně testujeme jejich významnost.
Obecný lineární model
Jistým zobecněním a zapouzdřením výše uvedených metod je použití obecného
lineárního modelu (GLM = General Linear Model). Jedná se vlastně o určité
zobecnění lineární regresní analýzy. Ovšem dle způsobu sestavení modelu a
následného testování a interpretace regresních koeficientů z něj získáme
např. t-test nebo ANOVu. Základní koncepce je znázorněna na následujícím obrázku.
Maticový zápis obecného lineárního modelu a jeho grafickou reprezentaci
pak můžeme vidět na dalším obrázku.
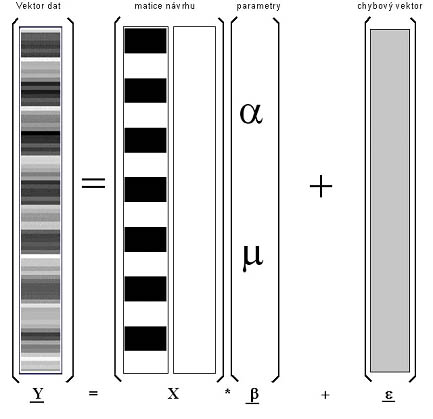
Výsledný statistický obraz (tzv. statistickou parametrickou mapu) získáme tak,
že provedeme odhad parametrů modelu a výpočet příslušné testové statistiky.
K odhadu parametrů "beta" obecného lineárního modelu použijeme rovnici z
následujícího obrázku.

K výpočtu testové statistiky lze použít např. rovnici z následujícího obrázku
a to v případě požadavku na t-statistiku (dále je možná F-statistika,
z-statistika atd. dle způsobu použití a interpretace).
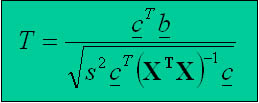
 počítadlo:
85990
počítadlo:
85990 CZ
CZ
 EN
EN

 nahoru
nahoru
 domů
domů